Lisplog

Neil Munro: Ningle Tutorial 4: Forms

via Planet Lisp by on Fri, 28 Feb 2025 23:30:00 GMT

Contents

• Part 1 (Hello World)
• Part 2 (Basic Templates)
• Part 3 (Introduction to middleware and Static File management)
• Part 4 (Forms)

Introduction

Welcome back, in this tutorial we will look at how to submit data back to our web application, this is typically done using forms. We will start by looking at the most basic way to do it, with templates and using ningle controllers, then we will look into using a package called cl-forms. As we do so we will also look into security concerns, specifically cross site request forgery (csrf) and how to implement it.

I made a small contribution to cl-forms as part of this tutorial, as a result the version required for this tutorial may not yet be available in quicklisp so you may want to consider using git to clone it into your quicklisp/local-projects directory.

If you are uncomfortable with, or would like to review how http messages work, please consult this article on mdn, it will be important to understand how forms in html work.

We will concern ourselves with creating the beginnings of an authentication app, our form will allow a user to submit an email address, and their password twice (once to confirm it's been entered correctly), at the end of this tutorial, you will be able to serve a form and accept the submitted user data back.

We will also consider csrf security tokens, which is a common security practice and it is very important to ensure we take security seriously, even when learning!

Ningle Basic Forms

While we will look into how to use forms in ningle using basic requests, responses, and html here, it is included only as an example, the tutorial project will not use this method, instead using cl-forms.

To begin with, we shall create a html file that will represent our form, in our templates directory, we will create a file called register.html with the following content:

{% extends "base.html" %}

{% block content %}
    <h1>Register for an account</h1>
    <form action="/register" method="POST">
        <label for="username">Username</label>
        <input type="email" name="username" id="username" />

        <label for="password1">Password</label>
        <input type="password" name="password1" id="password1" />

        <label for="password2">Confirm Password</label>
        <input type="password" name="password2" id="password2" />
        
        <input type="submit" value="Register" />
    </form>
{% endblock %}

We will immediately write our ningle controllers to render this form and an view to simply print out the data submitted in the form, there's two ways you can do this, you can handle the GET and POST requests independently, or you can have one controller that does both. I will show both methods, for clarity, with some reasons of why you might pick one over the other, but I will use one controller to handle both GET and POST requests.

You might want to write separate controllers for each method to separate concerns, it may not be obvious from this example, but controllers and processing can get quite complicated, you might want to consider splitting the different logic up. The thing to notice is that there's a slight change to the line to bind a controller to a route, the :method :GET and :method :POST addition, these are required and the default is :method :GET, but in order to enable other http methods you must include any additional methods.

You may find it cleaner to separate out controllers in this manner, at the expense of writing out some extra boiler plate, personally, I quite like this, but I'm very used to the alternative method of combining both into one. I reserve the right to change my mind later!

(setf (ningle:route *app* "/register" :method :GET)
    (lambda (params)
        (djula:render-template* "register.html" nil)))

(setf (ningle:route *app* "/register" :method :POST)
    (lambda (params)
        (format t "Username: ~A~%" (cdr (assoc "username" params :test #'string=)))
        (format t "Password: ~A~%" (cdr (assoc "password1" params :test #'string=)))
        (format t "Confirm: ~A~%" (cdr (assoc "password2" params :test #'string=)))
        (djula:render-template* "register.html" nil)))

The alternative is a little bit less boiler plate, and you can tell ningle to accept multiple http methods with :method '(:GET :POST) (without accepting both it will only take one or the other), the thing we will have to bear in mind is that where previously we could know for certain we only had one type of request and we could write code only to deal with a GET or POST, here we might have to check what the nature of the request is, and conditionally perform some logic. The lack.request package has a method we can use to determine this: (lack.request:request-method ningle:*request*), this will return a string representation of the request method, in our example below "POST". If we detect a POST request we will print out (using format) the values stored in the request body.

(setf (ningle:route *app* "/register" :method '(:GET :POST))
    (lambda (params)
        (when (string= "POST" (lack.request:request-method ningle:*request*))
            (format t "Username: ~A~%" (cdr (assoc "username" params :test #'string=)))
            (format t "Password: ~A~%" (cdr (assoc "password1" params :test #'string=)))
            (format t "Confirm: ~A~%" (cdr (assoc "password2" params :test #'string=))))
        (djula:render-template* "register.html" nil)))

In both examples we have to use this (cdr (assoc "username" params :test #'string=)) (or whatever input field we want) to retrieve the values stored in the form inputs, the params object is used for url information and body parameters.

Using whichever of these methods, you should save, reload, and restart your project access it in your web browser, if you navigate to /register, your form should render. Fill in a username, and the two password fields, when you look at the terminal output, you should see the values printed out.

As impressive as this is, we need to ensure that our application is secure and we must setup "cross site request forgery" (csrf) protection. In a nutshell, this creates a unique string send as a hidden input, and is rendered inside the form, if the application does not receive its csrf token back, it can be assumed that the request has been tampered with and isn't considered safe and the request should be rejected. It's a simple, but effective security measure that you absolutely should implement when rendering forms and accepting data from them.

You can read more about csrf at the OWASP Page.

The first thing to do, we must enable the default lack middleware modules session and csrf, in our lack.builder we must modify it to look like this.

(lack.builder:builder :session
                      :csrf
                      (:static
                        :root (asdf:system-relative-pathname :ningle-tutorial-project "src/static/")
                        :path "/public/")
                      *app*)

The :session middleware module should be loaded prior to :csrf, this is because the csrf module stores information in the session object, which wont exist if the session isn't first initialised. The csrf middleware module gives us a function we can call that will give us a hidden html tag we can render in our template, but of course we must pass it into the template, we must edit the controller like so:

(setf (ningle:route *app* "/register" :method '(:GET :POST))
    (lambda (params)
        (when (eq :POST (lack.request:request-method ningle:*request*))
            (format t "Username: ~A~%" (cdr (assoc "username" params :test #'string=)))
            (format t "Password: ~A~%" (cdr (assoc "password1" params :test #'string=)))
            (format t "Confirm: ~A~%" (cdr (assoc "password2" params :test #'string=))))
        (djula:render-template* "register.html" nil :csrf (lack/middleware/csrf:csrf-html-tag ningle:*session*))))

On the final line, the render-template* function is edited to be passed a csrf keyword argument, there's other functions such as csrf-token, however, the csrf middleware module can be configured to change the name of the token (if that's what you want to do), and so having the csrf-token isn't enough, you'd need to know what it's called internally to send the right name back, rendering the html tag simplifies this.

Finally we will need to update our template to include this tag:

{% extends "base.html" %}

{% block content %}
    <h1>Register for an account</h1>
    <form action="/register" method="POST">
        {{ csrf|safe }}
        <label for="username">Username</label>
        <input type="email" name="username" id="username" />

        <label for="password1">Password</label>
        <input type="password" name="password1" id="password1" />

        <label for="password2">Confirm Password</label>
        <input type="password" name="password2" id="password2" />
        
        <input type="submit" value="Register" />
    </form>
{% endblock %}

We must remember to pipe the csrf data though the safe filter so that it is rendered as html and not simply printed to the browser. This will create a hidden input in our form, it should have the name _csrf_token, it is possible to change this, if you wish, by altering the use of :csrf in the lack.builder line.

(lack.builder:builder :session
                      (:csrf :form-token "csrf-protection-token")
                      (:static
                        :root (asdf:system-relative-pathname :ningle-tutorial-project "src/static/")
                        :path "/public/")
                      *app*)

By changing the csrf middleware setup to a list and adding the :form-token keyword you should be able to see when you restart your project that the hidden input name is now csrf-protection-token.

CL-Forms

Having now seen how forms can be done using just requests, responses, and html, we can look at a package called cl-forms, which will enable us to define what our forms will be in Common Lisp code, it may seem unusual to prepare in the backend what is typically presented by html, however the cl-forms package offers validation and an easier way to retrieve data, as well as handling the csrf for us.

We will be using cl-forms as the default way to handle forms in the tutorial, so while the above section is worth understanding, and may come in helpful under some circumstances, this tutorial will only use cl-forms.

Unlike before where we just started writing html, we need to install and setup cl-forms, it has multiple ways to configure it, and we need to use the ningle backend.

In our project asd file we need to add the following cl-form dependencies:

1. cl-forms
2. cl-forms.djula
3. cl-forms.ningle

The full dependencies section should look like the following:

:depends-on (:clack
               :ningle
               :djula
               :cl-forms
               :cl-forms.djula
               :cl-forms.ningle)

It is not sufficient to just depend on cl-forms, it has multiple packages, and we want to use the djula template system and the ningle backend, so we must also include these else we may end up using the wrong implementations of some methods. The, cl-forms.djula package, for example, includes some djula tags that we will use in rendering our form and we must ensure these are loaded into our project otherwise we will get errors attempting to render the form.

You might also be tempted to enable the csrf middleware while we are editing this file, however cl-forms has its own implementation of csrf tokens and it conflicts with the ningle csrf middleware, so we do not need to implement it, in fact it will break things if we do.

As before, we will begin by editing our register.html file, however the content will be much simpler, all we will do is use a tag to render the form in one line.

{% extends "base.html" %}

{% block content %}
    <h1>Register for an account</h1>
    {% form form %}
{% endblock %}

This is a considerable amount of code we now don't have to write in our frontend templates! The {% form form %} instructs a form object to render its contents using djula (the templating package from the previous tutorial), as mentioned above the form tag is included as part of cl-forms.djula and this is why we had to depend on it.

Instead of declaring all the form fields using html, instead we can write a Lisp class that will be displayed for us, it will also handle the csrf token for us, we do not need to explicitly send it, the cl-forms package will do it for us.

That class will be written to forms.lisp, for now we will just write a basic register form, it will only include an email field, and two password fields (one will be to verify the first).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
(defpackage ningle-tutorial-project/forms
  (:use :cl)
  (:export #:register
           #:email
           #:password
           #:password-verify))

(in-package ningle-tutorial-project/forms)

(cl-forms:defform register (:action "/register" :id "signup" :csrf-protection t :csrf-field-name "csrftoken")
  ((email :email :value "")
   (password :password :value "")
   (password-verify :password :value "")
   (submit :submit :label "Register")))

Declaring a form is very similar to declaring a regular class, as the defform macro provided by cl-forms creates the accessor methods like defclass does. We do need to provide an action (which is where we want the url to send the form data to), and it's possible to pass in html attributes, but there's also the :csrf and :csrf-field-name keyword arguments, these are optional and instruct the form to include a hidden html field, something that we had to do manually using purely html.

Each attribute in the form is laid out similarly to class attributes, however taking the first field as an example (email :email :value "") this sets the form input element to have a name of email (the first item in the list), and it sets the input type to be of email, this is the second argument :email, you can see other form items have :password which maps onto a password input type. The value attribute allows you to set a value on the form input element. It's worth noting that arbitrary attributes such as id, class etc can't be set here, but the name, the type and value are all derived from the Common Lisp form attributes.

We can also set up the fields and a submit button in the defform macro, setting up values etc, there's much more that the defform can do, and I strongly suggest you have a look at the demo, we will explore more uses of defform later in this tutorial series, for now we will just connect up this form to the rest of our application and confirm everything is working first.

With the cl-forms package installed, the form class set up and the html written, there is only one final thing left to do, we need to expand our controller to load the form and send/recieve data.

One thing to remember though, because the form was defined in another file, and indeed in another package, we must either:

• Use the package
• Import the exported symbols
• Explicitly use symbols

I personally choose to import exported symbols, but that's from a almost 20 years of working with Python!

To achieve this, if you want to just use the form package, in the defpackage section at the top:

(defpackage ningle-tutorial-project
  (:use :cl :ningle-tutorial-project/forms)
  (:export #:start
           #:stop))

If you wish to import exported symbols:

(defpackage ningle-tutorial-project
  (:use :cl)
  (:import-from
   :ningle-tutorial-project/forms
   #:register
   #:email
   #:password
   #:password-verify)
  (:export #:start
           #:stop))

If, however, you want to just explicitly use the symbols, we will need to look at as we come to specific areas of code.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
(setf (ningle:route *app* "/register" :method '(:GET :POST))
    (lambda (params)
        (let ((form (cl-forms:find-form 'register)))
          (if (string= "GET" (lack.request:request-method ningle:*request*))
            (djula:render-template* "register.html" nil :form form)
            (handler-case
                (progn
                    (cl-forms:handle-request form) ; Can throw an error if CSRF fails
                    (multiple-value-bind (valid errors)
                        (cl-forms:validate-form form)
                      (when errors
                        (format t "Errors: ~A~%" errors))
                      (when valid
                        (cl-forms:with-form-field-values (email password password-verify) form
                            (format t "Testing: email - ~A, password - ~A, password-verify - ~A~%" email password password-verify)))
                    (djula:render-template* "register.html" nil :form form)))

                (simple-error (csrf-error)
                    (setf (lack.response:response-status ningle:*response*) 403)
                    (djula:render-template* "error.html" nil :error csrf-error)))))))

This is quite a lot more code that any of our previous controllers, as discussed in the previous section, on line 1, we must include :method '(:GET :POST) in our routing. This allows the form to be initially rendered in the GET http request and data interpreted on the server with POST http request.

Within our controller, on line 3 we use cl-forms to load the form with find-form (passing in the symbol that references the form), since we will use this form in a number of places. This will represent both the blank form rendered from the GET request and the populated form submitted in the POST request.

Line 4 is a simple check to determine with type of request we are dealing with, if the string "GET" returned by the lack.request:request-method function then the form will just be rendered with djula. With a simple if used in the code here, you might be interested to know that there are in fact 9 http methods:

1. CONNECT
2. DELETE
3. GET
4. HEAD
5. OPTIONS
6. PATCH
7. POST
8. PUT
9. TRACE

If there's so many, why are we only use a simple if? Because of the :method '(:GET :POST)! With that we explicitly define which methods this controller will accept and we don't need to worry about the other 7 methods, and as such, a simple if is all we need in this instance.

Using only this if, line 6 begins the else clause of it, here is where things begin to get interesting! We begin with a handler-case, if you have used other languages that take advantage of Exception Handling, it's analogous to that, and you may want to skip the explaination.

If not, expand this for more details on handler-case!

    handler-case is a Common Lisp macro that, in simple terms, allows us to attempt to execute a block of code, on the understanding that it may fail, and if that happens, depending on the nature of the failure, we might want to run some other code to handle the error.

    Let's look at a simple example:
    
    (defun div (a b)
        (/ a b))

    (div 1 2)


    A very simple function here "div" takes an "a" and a "b" and attempts to divide them, everything should work fine for the first call, returning 1/2 (0.5, 50%), however if you call it with the second number being 0, the interpreter signals a DIVISION-BY-ZERO error, which is correct, without wanting to go down a mathematical tangent, computers generally can't divide by zero, so throwing an error is a logical thing to do. 

    So how can we recover from this situation? We don't want to drop into the debugger and manually handle things every time there's an error! This is what handler-case allows us to do. We start with what we want to do, in this case (/ a b), this is the first form we pass to handler-case, but we also pass in 0 or more "error-clauses".
    
    (defun div (a b)
        (handler-case (/ a b)
        (division-by-zero (e)
            (format nil "Can't divide by zero"))))

    (div 1 2)
    (div 1 0)


    We pass in an "error-clause" that captures the condition type, in this case a division-by-zero, "error-clauses" take a condition name (remembering exceptions are a type of condition) and the condition object (which I called "e"), and perform some other code, since the original intended functionality cannot be completed.

    When we pass "0" in as the second argument, we now get the string "Can't divide by zero" returned from the function, which is much better, but what if I pass in something that isn't even a number?
    
    (div 1 "a")


    Well, this time I get a new exception signalled, a type-error, which with a small modification:
    
    (defun div (a b)
        (handler-case (/ a b)
        (type-error (e)
            (format nil "Something isn't a number"))

        (division-by-zero (e)
            (format nil "Can't divide by zero"))))

    (div 1 2)
    (div 1 0)
    (div 1 "a")


    With the new "error-clause" added, this function can now handle some exceptional circumstances!
    
    Something to bear in mind however is that the initial form to handler-case expects a single form, which is why we may have to use a progn to wrap multiple expressions in one form. Of course a let would work just as well, but in my code there's nothing to bind in the let, so a progn would do.
    

If the csrf token does not match the handle-request function will signal an error condition and the code in the error-clause will run (lines 18-20), the http status code will be set to 403 Forbidden and our error template will be rendered with the error object being passed to the template.

Assuming the csrf token has not been tampered with and no error is signalled, our code will run through lines 7-16, the progn will enclose all of our logic and the handle-request will bind the field values the user entered to the form object, which will then enable us to validate the form.

To validate the form we must call the validate-form function in cl-forms package. According to the documentation it returns the result of a call to values and returns two, a generalized boolean representing if the form is valid or not, and a list of errors. Typically if the form is valid there shouldn't be any errors and vice versa.

To take advantage of the multiple values returned from validate-form we should use a multiple-value-bind form.

For a recap of values and multiple-value-bind, click here!

    Sometimes you want a function to return multiple values, in some languages (like Python), this basically is returning an implicit tuple that is unpacked, in Common Lisp it is different, and more nuanced. The function values returns a special type of object that, if accessed only returns the first value, however there are other values that may be useful, but perhaps not always.
    
    A simple example is using the floor division if we try to divide 1 by 2, we end up with 0 and 1 remainder. Therefor (floor 1 2) will give 0, except it doesn't! It actually returns 0, 1, the 0 and the 1 remainder.
    
    Proving that, however, the 0 is returned by default, we can do the following:
    
    
(+ 4 (floor 1 2))
 
    
    Which will give us the value of 4, since the result of (floor 1 2) is a special kind of object that holds multiple values but only gives you the first one, we basically have 4 + 0 here, which is quite correct. You might be wondering then, if we only ever get the first value... how do we get the rest?
    
    Enter multiple-value-bind!
    
    multiple-value-bind is a macro that allows us to capture all values and use them.
    
    

    (multiple-value-bind (quotient remainer)
        (floor 1 2)
      (format t "Dividing 1 by 2 gives ~A with ~A remaining!~%" quotient remainder))
    
    Here, with our floor division example from above, we capture the quotient (how many times a number can be wholly divided) and remainder (how much remains that cannot be evenly divided) in the first form that multiple-value-bind takes, the next form must be the expression that returns a values list, it is very important to note that ALL of the returned values are listed in the first form, even if you won't be using them!
    
    Once this binding has been done, you may have as many expressions as you like inside the multiple-values-bind after the second form, all subsequent expressions are wrapped in an implicity progn.
    

Using the multiple-value-bind we are able to capture the valid and errors values returned from (cl:forms:validate-form form) call on line 10.

At this point in the tutorial we don't have any way for a html form to be invalid so errors won't be captured, however this is something we will come back to, so the line lines 11-12 are there to display any errors we will receive later in this tutorial, although do remember all we are doing with this tutorial is displaying messages in the terminal!

Given there's no errors to be signalled (yet) the form can be assumed to be valid and we will simply display a string in the terminal with the values the form received on lines 13-15. One thing to note is that similarly to the multiple-value-bind macro, cl-forms provides a with-form-field-values macro that given a list of fields and a form, it will bind the values of the fields of the form and allow you to access the user submitted data.

The fields must be known to the package and is why I was clear earlier about needing to import or use the form package. You could, of course access the members directly, but this is a lot of typing ('ningle-tutorial-project/forms:email instead of email for example). In Common Lisp you are of course free to construct your packages as you see fit, so if another way of arranging your code works for you by all means use that!

Finally, we render the template on line 16, as before!

If we start this application and navigate to /register then we should see the form we have defined in forms.lisp being rendered as expected. If you fill in the form, you should find that if you attempt to put something other than an email into the email field you will get the browser informing you that an email field must contain an email, which is good! This tells us that our form is being rendered as we wanted it to, using the correct html form elements! To continue, if you fill in the form and submit it, looking into the terminal should show us the data you entered, and if so, congratulations!

Now, about those lack of errors... it's possible to enter pathetic passwords into our form and we should be taking security seriously, we must talk about form validation!

A distinct advantage that using cl-forms over writing your own html forms is that while it is possible to validate the form on the client side (the web browser) if someone were to bypass the client and send data directly to your web server, it could be valid data, but it could also be invalid data (possibly a problem), or even malicious (definitely a problem!), having client side validation is no substitute for validating in the backend. A common adage in computer science "never trust user input", so we mustn't. I could attempt to convince you instead I'll just embed this.

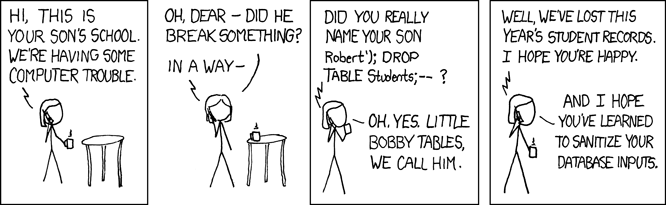
Never trust incoming data.

So, given the password fields allow for weak passwords, what can we do about it?

Clavier is a validation library that cl-forms depends on and we can use to validate the form data. It's a pretty low level validation library, but since cl-forms is designed to use it, integrating it is rather easy. We already wrote some code in our controller to handle errors, should they occur, so the only thing we need to do is edit our form to put our validation constraints in place. Clavier comes with individual validators and ways to combine them (&& and || for and-ing and or-ing, for example), the library has all the basic building blocks of validation that I could think of wanting.

To integrate it into our form, we must provide a ":constraints" keyword argument, which must be a list of each specific constraint we want to use, and since we are validating our password, we need to use this twice so I chose to store it as a variable.

In this example, I'm going to ensure a password:

1. Can't be blank
2. Is a string
3. Is at least 8 characters long

We could also add some checks for upper and lower case letters, numbers, and special characters, and there is a regex validator that we can use to achieve that, but that's an exercise for another tutorial!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
(defpackage ningle-tutorial-project/forms
  (:use :cl)
  (:export #:register
           #:email
           #:password
           #:password-verify
           #:*password-validator*))

(in-package ningle-tutorial-project/forms)

(defparameter *password-validator* (list (clavier:not-blank)
                                         (clavier:is-a-string)
                                         (clavier:len :min 8)))

(cl-forms:defform register (:action "/register" :id "signup" :csrf-protection t :csrf-field-name "csrftoken")
  ((email :email :value "")
   (password :password :value "" :constraints *password-validator*)
   (password-verify :password :value "" :constraints *password-validator*)
   (submit :submit :label "Register")))

This is the complete listing of the forms.lisp file, as mentioned above, the only real change is creating a list of the validators we might want to use and passing them as the keyword argument. If you save all of this and start the project, you can experiment with submitting the register form with valid data, in which case you will get the information printed in the terminal. Or if you submit the form with invalid data you will see the error printed in the terminal, but you will also have the errors displayed in the web browser as seen below.

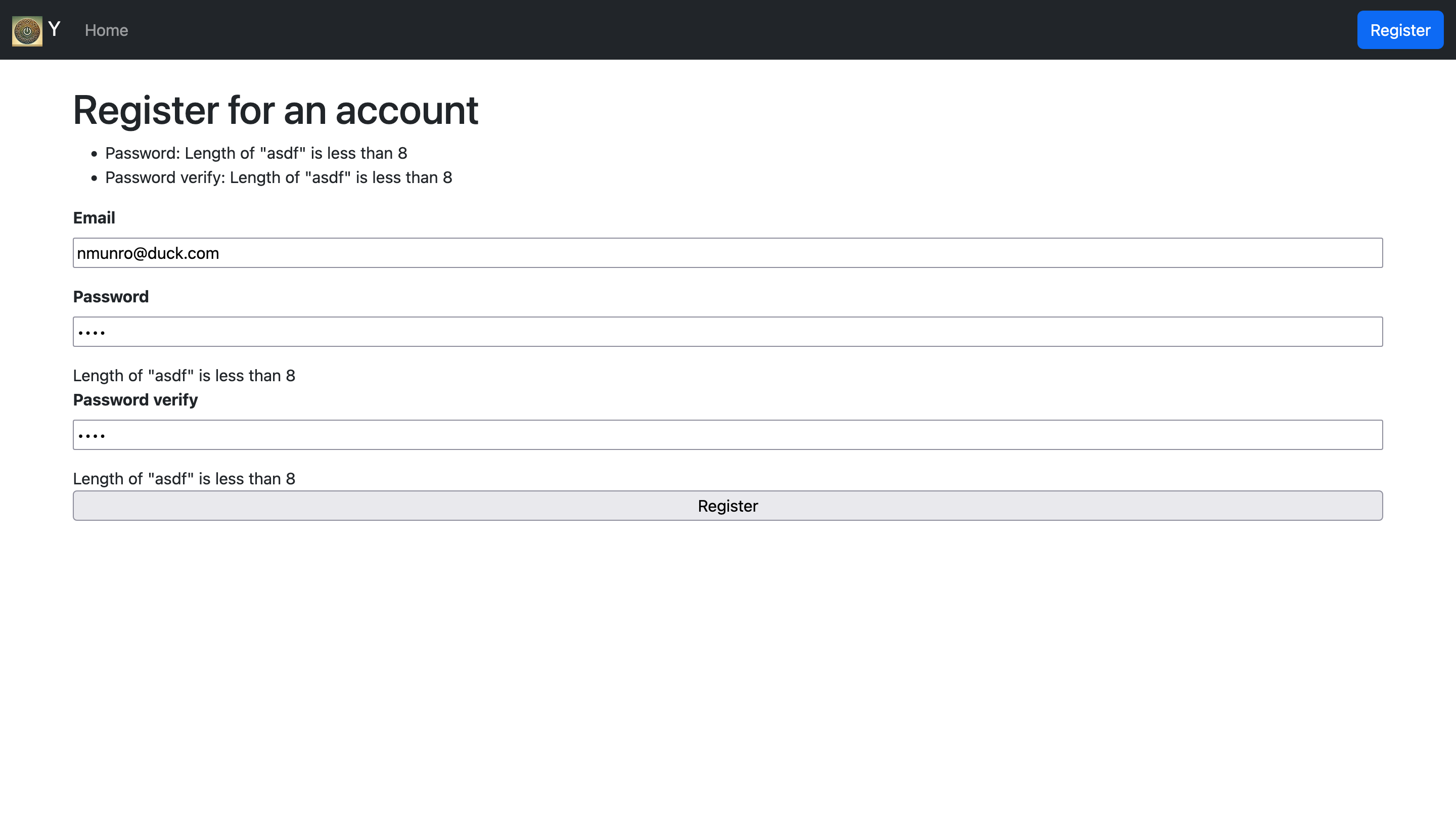
You might be wondering, if this screenshot appears automatically for us, why we might also want to log errors, in this small example it doesn't make much sense, but in production you certainly might want to know if repeated attempts to create user accounts are failing, it could be some sort of cyber attack, or some other malicious actor probing your application and you would certainly want to know about that!

And with that, we come to the end of this tutorial, I hope you have found this helpful and are enjoying this tutorial series.

Conclusion

To recap, after working your way though this tutorial you should be able to:

• Use html to render a form
• Use cl-forms to render a form
• Explain what http messages are, specifically get and post
• Explain why cl-forms is a better choice than html
• Explain what Cross Site Request Forgery (csrf) tokens are and how they help security
• Use csrf tokens to prevent a csrf vulnerability
• Handle submitting a form using html
• Handle submitting a form using cl-forms
• Use clavier to validate a form
• Handle errors signalled from clavier

Github

The link for this tutorial code is available here.

Resources

• 403 Status
• clavier
• cl-forms
• cl-forms demo
• cl-forms validate-form
• condition
• CSRF Explained
• DIVISION-BY-ZERO
• error
• Exception Handling
• handler-case
• Http Messages
• multiple-value-bind
• type-error
• XKCD 327: Exploits Of A Mom

;;; -*- Lisp -*-

(in-package "ADVENT2024/DAY17")

(defstruct (machine
            (:type vector)
            (:conc-name machine/))
  (pc 0)
  a
  b
  c
  (program (vector) :read-only t))

(defun read-machine (filename)
  (apply #’make-machine
         (collect-append
          (choose
           (#M(lambda (line)
                (cond ((str:starts-with? "Register A:" line)
                       (list :a (parse-integer (subseq line 11))))
                      ((str:starts-with? "Register B:" line)
                       (list :b (parse-integer (subseq line 11))))
                      ((str:starts-with? "Register C:" line)
                       (list :c (parse-integer (subseq line 11))))
                      ((str:starts-with? "Program:" line)
                       (list :program (collect ’vector
                                        (choose
                                         (#Mdigit-char-p
                                          (scan ’string (subseq line 9)))))))
                      (t nil)))
              (scan-file filename #’read-line))))))

(defun run-machine (machine)
  (symbol-macrolet ((a  (machine/a machine))
                    (b  (machine/b machine))
                    (c  (machine/c machine))
                    (pc (machine/pc machine))
                    (program (machine/program machine))
                    (immediate (svref program (1+ pc)))
                    (argument (ecase immediate
                                (0 0)
                                (1 1)
                                (2 2)
                                (3 3)
                                (4 a)
                                (5 b)
                                (6 c)))
                    (next-instruction (progn (incf pc 2)
                                             (iter))))

    (let ((output ’()))
      (let iter ()
        (if (>= pc (length program))
            (reverse output)
            (ecase (svref program pc)
              (0 (setf a (truncate a (expt 2 argument))) next-instruction)
              (1 (setf b (logxor b immediate))           next-instruction)
              (2 (setf b (mod argument 8))               next-instruction)

              (3
               (if (zerop a)
                   next-instruction
                   (progn
                     (setf pc immediate)
                     (iter))))

              (4 (setf b (logxor b c))                   next-instruction)
              (5 (push (mod argument 8) output)          next-instruction)
              (6 (setf b (truncate a (expt 2 argument))) next-instruction)
              (7 (setf c (truncate a (expt 2 argument))) next-instruction)))))))

(defun part-1 ()
  (format nil "~{~d~^,~}" 
    (run-machine (read-machine (input-pathname)))))

(defun get-machine-state (machine)
  (list (machine/pc machine)
        (machine/a machine)
        (machine/b machine)
        (machine/c machine)))

(defun set-machine-state! (machine state)
  (setf (machine/pc machine) (first state)
        (machine/a machine) (second state)
        (machine/b machine) (third state)
        (machine/c machine) (fourth state)))

(defun try-machine (machine state input-a)
  (set-machine-state! machine state)
  (setf (machine/a machine) input-a)
  (run-machine machine))

(defun pad-terms (terms size)
  (revappend (make-list (- size (length terms)) :initial-element 0) terms))

(defun from-octal (octal-digits)
  (fold-left (lambda (n digit) (+ (* n 8) digit)) 0 (reverse octal-digits)))

(defun part-2 ()
  (let* ((machine (read-machine (input-pathname)))
         (initial-state (get-machine-state machine))
         (target (machine/program machine)))
    (let term-loop ((terms ’())
                    (index (1- (length target))))
      (if (= index -1)
          (from-octal terms)
          (let digit-loop ((digit 0))
            (if (> digit 7)
                (error "No solution")
                (let* ((padded (pad-terms (cons digit terms) (length target)))
                       (output (try-machine machine initial-state (from-octal padded))))
                  (if (and (= (length output) (length target))
                           (= (elt output index) (svref target index)))
                      (term-loop (cons digit terms) (1- index))
                      (digit-loop (1+ digit))))))))))

Joe Marshall: Advent of Code 2024: Day 16

via Planet Lisp by on Thu, 27 Feb 2025 08:00:00 GMT

For day 16, we are solving a maze. We want to find the lowest cost path from the start to the end. Taking a step straight ahead costs 1, but turning left or right costs 1000.

This puzzle was the most vexing of all the puzzles. The solution is straightforward but the devil is the details. I found myself constantly mired in the CARs and CDRs of the path data structure, descending too far or not far enough. I tried several different representations for a path, each one with its own set of problems. Trying to keep track of the direction of the steps in the path turned out to be an exercise in frustration.

The algorithm is a variant of Dijkstra’s algorithm, which finds the shortest weighted path in a graph. In our case, the graph is derived from the maze. The vertices of the graph are the locations in the maze with three or more paths leading out of them. The edges in the graph are the steps between the vertices. But you cannot compute the cost of a path by summing the weights of the edges, as the final edge in the path may be reached either by proceeding straight through the prior vertex, or by turing left or right at the prior vertex. Thus I modified Dijkstra's algorithm to be edge-oriented rather than vertex-oriented. This turned out to be a key to solving the problem. With the vertex-oriented solutions, I had to keep track of the orientation of the path as it entered and left the vertex, and annotating the steps along the path with their orientation turned into a bookkeeping nightmare. With the edge-oriented solution, I could discard the orientation information as I advanced the algorithm and reconstruct the orientation information only after I had generated a candidate path. This greatly simplified the bookkeeping.

The algorithm uses a pure functional weight-balanced binary tree as a priority queue for the paths. The tree is kept in order of increasing path score, so the lowest scoring path is always the leftmost path in the tree. In my original implementation, I punted and used a linear priority queue. This is simple, and it works, but is far too slow. The weight-balanced binary tree was cribbed from MIT-Scheme.

;;; -*- Lisp -*-

(in-package "ADVENT2024/DAY16")

(defun read-input (input-pathname)
  (read-file-into-grid
    (char-interner #’identity (find-package "ADVENT2024/DAY16"))
     input-pathname))

(defun start-and-goal (maze)
  (let ((inverse (invert-grid maze ’|.|)))
    (values (first (gethash ’S inverse))
            (first (gethash ’E inverse)))))

Since Dijkstra’s algorithm is a graph algorithm, we need to represent the maze as a graph. We simplify the graph by flooding the dead ends.

(defun dead-end? (maze coord)
  (and (on-grid? maze coord)
       (eql (grid-ref maze coord) ’|.|)
       (let ((n (coord-north coord))
             (s (coord-south coord))
             (e (coord-east coord))
             (w (coord-west coord)))
         (let ((n* (or (not (on-grid? maze n))
                       (eql (grid-ref maze n) ’\#)))
               (s* (or (not (on-grid? maze s))
                       (eql (grid-ref maze s) ’\#)))
               (e* (or (not (on-grid? maze e))
                       (eql (grid-ref maze e) ’\#)))
               (w* (or (not (on-grid? maze w))
                       (eql (grid-ref maze w) ’\#))))
           (or (and n* e* w*)
               (and e* n* s*)
               (and s* e* w*)
               (and w* n* s*))))))

(defun flood-dead-end! (maze coord)
  (when (dead-end? maze coord)
    (setf (grid-ref maze coord) ’\#)
    (flood-dead-end! maze (coord-north coord))
    (flood-dead-end! maze (coord-south coord))
    (flood-dead-end! maze (coord-east coord))
    (flood-dead-end! maze (coord-west coord))))

(defun flood-dead-ends! (maze)
  (iterate ((coord (scan-grid-coords maze)))
    (flood-dead-end! maze coord)))

We then mark the vertices of the graph by looking for locations with three or more paths leading out of them.

(defun vertex? (maze coord)
  (and (on-grid? maze coord)
       (eql (grid-ref maze coord) ’|.|)
       (let ((n (coord-north coord))
             (s (coord-south coord))
             (e (coord-east coord))
             (w (coord-west coord)))
         (let ((n* (and (on-grid? maze n) (member (grid-ref maze n) ’(\. + S E))))
               (s* (and (on-grid? maze s) (member (grid-ref maze s) ’(\. + S E))))
               (e* (and (on-grid? maze e) (member (grid-ref maze e) ’(\. + S E))))
               (w* (and (on-grid? maze w) (member (grid-ref maze w) ’(\. + S E)))))
           (or (and n* e* w*)
               (and e* n* s*)
               (and s* e* w*)
               (and w* n* s*))))))

(defun mark-vertices! (maze)
  (let ((vertices ’()))
    (iterate ((coord (scan-grid-coords maze)))
      (when (vertex? maze coord)
        (setf (grid-ref maze coord) ’+)
        (push coord vertices)))
    vertices))

After flooding the dead ends and marking the vertices, all the edges begin and end at a vertex.

It isn’t necessary for the solution, but it helps to be able to visualize the maze. The show-maze procedure will print the maze to the standard output. The show-maze procedure takes an optional list of coords to highlight in the maze.

(defun show-maze (maze &optional highlight)
  (format t "~&")
  (dotimes (row (grid-height maze))
    (format t "~%")
    (dotimes (col (grid-width maze))
      (cond ((eql (grid-ref maze (coord col row)) ’\#)
             (format t "#"))
            ((member (coord col row) highlight :test #’equal)
             (format t "O"))
            ((eql (grid-ref maze (coord col row)) ’|S|)
             (format t "S"))
            ((eql (grid-ref maze (coord col row)) ’|E|)
             (format t "E"))
            ((eql (grid-ref maze (coord col row)) ’+)
             (format t "+"))
            (t
             (format t "."))))))

Between the vertices, we have the edges of the graph. An edge is simply the a list of coordinates between two vertices. The first and last coordinates of the edge are vertices. To find all the coordinates between two vertices, we walk the edge from the start until we reach another vertex. We don’t maintain direction. Instead, we just make sure that the new coordinate isn’t the last one in the edge we are walking so that we move forward.

(defun walk-edge (maze coord edge)
  (let ((n (coord-north coord))
        (s (coord-south coord))
        (e (coord-east coord))
        (w (coord-west coord)))
    (cond ((and (on-grid? maze n)
                (not (equal n (first edge)))
                (eql (grid-ref maze n) ’|.|))
           (walk-edge maze n (cons coord edge)))
          ((and (on-grid? maze n)
                (not (equal n (first edge)))
                (member (grid-ref maze n) ’(+ S E)))
           (list* n coord edge))
          ((and (on-grid? maze e)
                (not (equal e (first edge)))
                (eql (grid-ref maze e) ’|.|))
           (walk-edge maze e (cons coord edge)))
          ((and (on-grid? maze e)
                (not (equal e (first edge)))
                (member (grid-ref maze e) ’(+ S E)))
           (list* e coord edge))
          ((and (on-grid? maze s)
                (not (equal s (first edge)))
                (eql (grid-ref maze s) ’|.|))
           (walk-edge maze s (cons coord edge)))
          ((and (on-grid? maze s)
                (not (equal s (first edge)))
                (member (grid-ref maze s) ’(+ S E)))
           (list* s coord edge))
          ((and (on-grid? maze w)
                (not (equal w (first edge)))
                (eql (grid-ref maze w) ’|.|))
           (walk-edge maze w (cons coord edge)))
          ((and (on-grid? maze w)
                (not (equal w (first edge)))
                (member (grid-ref maze w) ’(+ S E)))
           (list* w coord edge)))))

Given a vertex, we can find all the edges that lead out of that vertex.

(defun vertex-edges (maze vertex)
  (let ((n (coord-north vertex))
        (s (coord-south vertex))
        (e (coord-east vertex))
        (w (coord-west vertex))
        (edges ’()))
    (when (and (on-grid? maze n) (member (grid-ref maze n) ’(|.| + S E)))
      (push (walk-edge maze n (list vertex)) edges))
    (when (and (on-grid? maze s) (member (grid-ref maze s) ’(|.| + S E)))
      (push (walk-edge maze s (list vertex)) edges))
    (when (and (on-grid? maze e) (member (grid-ref maze e) ’(|.| + S E)))
      (push (walk-edge maze e (list vertex)) edges))
    (when (and (on-grid? maze w) (member (grid-ref maze w) ’(|.| + S E)))
      (push (walk-edge maze w (list vertex)) edges))
    edges))

Given the ordered list of coords in a path through the maze, we need to be able to score it. There is a cost of 1 for every step, and a cost of 1000 for every turn. We calculate these separately.

To find the directions of the steps in the path, we examine adjacent coords. If the columns are the same, the direction is north/south. If the rows are the same, the direction is east/west. The very first direction is east/west because the start is always facing east. Once we have a sequence of the directions, we examine adjacent directions to see if they are the same. If they are, we went straight, otherwise we turned.

(defun count-turns (coord-list)
  (multiple-value-bind (bs as)
      (chunk 2 1 (multiple-value-bind (ls rs) (chunk 2 1 (scan ’list coord-list))
                   (catenate (#M(lambda (l r)
                                  (cond ((= (column l) (column r)) ’ns)
                                        ((= (row l) (row r)) ’ew)
                                        (t (error "Funky coord-list."))))
                                ls
                                rs)
                             (scan ’list (list ’ew)))))
    (collect-length (choose (#Mnot (#Meq bs as))))))

(defun score-coord-list (coord-list)
  (1- (+ (length coord-list)
         (* 1000 (count-turns coord-list)))))

We represent a path as a list of edges. Given a list of edges, we need to stitch them together to create a list of coords in order to score the path. We cannot simply append the edges together, as the vertices between the edges will be duplicated. Instead, we drop the last coord (the ending vertex) from each edge except the first.

(defun at-goal? (path goal)
  (equal (first (first path)) goal))

(defun path->coord-list (path)
  (if (null (rest path))
      (first path)
      (append (butlast (first path)) (path->coord-list (rest path)))))

Given a path, we can extend it by finding the edges that lead out of the last vertex in the path. We discard the edge that came into the vertex, as we don’t want to backtrack.

(defun path-extensions (maze path)
  (let* ((latest-edge (first path))
         (latest-vertex (first latest-edge))
         (back-edge (reverse latest-edge))
         (outgoing-edges (remove back-edge (vertex-edges maze latest-vertex) :test #’equal)))
    (map ’list (lambda (edge) (cons edge path)) outgoing-edges)))

As I mentioned earlier, we use a weight-balanced binary tree as a priority queue. I didn’t bother trying to abstract this. I’m just manipulate the raw nodes of the tree. Each node has a key, which is the score, and a value, which is a list of paths that have that score. We compare keys with the < function. Weight-balanced binary trees are pure functional — adding or popping the queue returns a new queue rather than side effecting the existing one.

(defun make-priority-queue ()
  wtree::empty)

(defun pq-insert (pq entry score)
  (let* ((probe (wtree::node/find #’< pq score)))
    (wtree::node/add #’< pq score (cons entry (and probe (wtree::node/v probe))))))

(defun pq-pop (pq)
  (let* ((node (wtree::node/min pq))
         (score (wtree::node/k node))
         (value-list (wtree::node/v node))
         (value (car value-list))
         (tail (cdr value-list)))
    (if (null tail)
        (values value score (wtree::node/delmin pq))
        (values value score (wtree::node/add #’< (wtree::node/delmin pq) score tail)))))

We finally arrive at the solve-maze procedure. This proceeds in three parts. First, we prepare the maze by flooding the dead ends and marking the vertices. We initialize visited-edges which is a hash table mapping an edge to the lowest score that has been found for a path ending in that edge. We initialize predecessor-edges which is a hash table mapping an edge to the edge that came before it in the lowest scoring path. The initial edges are the ones leading out of the start vertex, and the initial paths are the paths each containing one of the initial edges.

The second part is the main iteration. The outer iteration pops the lowest scoring path so far from the priority queue. If the path ends at the goal, we have found one solution and we proceed to part three where we collect other solutions that with the same score that end at the goal. Otherwise, we enter an inner loop over all ways we can extend the path by one edge. For each extension, we score the extension and look up the most recent edge in the visited-edges.

If we have not visited the edge before, we store the edge in visited-edges and store its predecessor in predecessor-edges. If we have visited the edge before, we have three cases. If the score of the extension is greater that the score we have seen before, we discard the extension. If the score of the extension is equal to the score we have see before, we add the edge preceeding the final edge to the predecessor-edges, but do not pursue this path further. If the score of the extension is less than the score we have previously found, we update the visited-edges with the new lower score and update the predecessor-edges so that this path is the only path leading to the final edge.

When we find a path that ends at the goal, we enter the third part of the procedure. We pop paths from the priority queue collecting any other paths that have also reached the goal with the same score. Finally, we return the list of shortest paths.

(defun solve-maze (maze)
  (flood-dead-ends! maze)
  (mark-vertices! maze)
  (multiple-value-bind (start goal)
      (start-and-goal maze)
    (let* ((visited-edges     (make-hash-table :test ’equal))
           (predecessor-edges (make-hash-table :test ’equal))
           ;; The initial edges are the ones that start at the start vertex.
           (initial-edges (vertex-edges maze start))
           ;; A path is a list of edges.  An initial path is a list of one edge starting at the start vertex.
           (initial-paths (map ’list #’list initial-edges)))

      (dolist (edge initial-edges)
        (setf (gethash edge visited-edges) (score-path (list edge))))

      ;; Main loop, iteratively extend the lowest scoring path.
      (let iter ((scored-paths (do ((pq (make-priority-queue) (pq-insert pq (car initial-paths) (score-path (car initial-paths))))
                                    (initial-paths initial-paths (cdr initial-paths)))
                                   ((null initial-paths) pq))))
        (unless (wtree::empty? scored-paths)
          (multiple-value-bind (path path-score next-scored-paths) (pq-pop scored-paths)
            (if (at-goal? path goal)
                ;; Reached the goal.  Keep popping until we have all solutions.
                (let solution-iter ((solutions (list path))
                                    (next-scored-paths next-scored-paths))
                  (if (wtree::empty? next-scored-paths)
                      solutions
                      (multiple-value-bind (other-path other-path-score next-scored-paths) (pq-pop next-scored-paths)
                        (if (= other-path-score path-score)
                            (solution-iter (if (at-goal? other-path goal)
                                               (cons other-path solutions)
                                               solutions)
                                           next-scored-paths)
                            (values solutions predecessor-edges)))))
                (let iter1 ((extensions (path-extensions maze path))
                            (next-scored-paths next-scored-paths))
                  (if (null extensions)
                      (iter next-scored-paths)
                      (let* ((extension (first extensions))
                             (extension-score (score-path extension))
                             (latest-edge (first extension))
                             (predecessor (second extension))
                             (prior-score (gethash latest-edge visited-edges)))
                        (cond ((null prior-score)
                               (setf (gethash latest-edge visited-edges) extension-score
                                     (gethash latest-edge predecessor-edges) (list predecessor))
                               (iter1 (rest extensions)
                                      (pq-insert next-scored-paths extension extension-score)))
                              ;; If we have found an extension with a worse score, we ignore it.
                              ((> extension-score prior-score)
                               (iter1 (rest extensions) next-scored-paths))
                              ;; If we have found an extension with an equal score, we add the predecessor,
                              ;; but do not pursue it further.
                              ((= extension-score prior-score)
                               (push predecessor (gethash latest-edge predecessor-edges))
                               (iter1 (rest extensions) next-scored-paths))
                              ;; If we have found an extension with a better score, we replace the prior extension.
                              ((< extension-score prior-score)
                               (setf (gethash latest-edge visited-edges) extension-score
                                     (gethash latest-edge predecessor-edges) (list predecessor))
                               (iter1 (rest extensions)
                                      (pq-insert next-scored-paths extension extension-score))))))))))))))

Of note is how the inner and outer iterations interact. The inner iteration is initialized with one of the loop variables of the outer loop. When the inner loop is done, it tail calls the outer loop with the loop variable it originally got from the outer loop. This gives the effect of the inner loop sharing a loop variable with the outer loop.

collect-minimum-coords collects all the coords along all minimal paths that lead through edges on the edge list.

(defun collect-minimum-coords (edge-list predecessor-table)
  (fold-left (lambda (coords edge)
               (union coords
                      (union edge (collect-minimum-coords (gethash edge predecessor-table) predecessor-table)
                             :test #’equal)
                      :test #’equal))
             ’()
             edge-list))

For part 1 of the puzzle, we solve the maze and return the score of a shortest path.

(defun part-1 ()
  (let ((maze (read-input (input-pathname))))
    (multiple-value-bind (paths predecessor-table) (solve-maze maze)
      (declare (ignore predecessor-table))
      (score-path (first paths)))))

For part 2 of the puzzle, we solve the maze and collect the coords of all the minimal paths that lead through the edges of the shortest paths.

(defun part-2 ()
  (let ((maze (read-input (input-pathname))))
    (multiple-value-bind (paths predecessor-table) (solve-maze maze)
      (let ((minimum-coords (collect-minimum-coords (map ’list #’first paths) predecessor-table)))
        (length minimum-coords)))))

;;; -*- Lisp -*-

(in-package "ADVENT2024/DAY15")

(defun decode-cell (string package wide?)
  (if wide?
      (cond ((equal string "#") (list ’\# ’\#))
            ((equal string "O") (list ’[ ’]))
            ((equal string ".") (list ’\. ’\.))
            ((equal string "@") (list ’@ ’\.))
            (t (error "Unknown cell ~a" string)))
      (list (intern (string-upcase string) package))))

(defun decode-move (move)
  (cond ((equal move "<") +west+)
        ((equal move "^") +north+)
        ((equal move ">") +east+)
        ((equal move "v") +south+)
        (t (error "Unknown move ~a" move))))

(defun read-input (input-pathname &optional; (wide? nil))
  (multiple-value-bind (blanks grids moves)
      (#3M(lambda (line)
            (cl-ppcre:register-groups-bind (blank grid move)
                ("(^$)|([#.O@]+)|([><v^]+)" line)
              (values blank grid move)))
          (scan-file input-pathname #’read-line))
    (let ((blank-lines (collect ’list (choose blanks)))
          (grid-lines  (collect ’list
                         (#M(lambda (line)
                              (collect-append (#Mdecode-cell
                                               (#Mstring (scan ’string line))
                                               (series (find-package "ADVENT2024/DAY15"))
                                               (series wide?))))
                            (choose grids))))
          (move-list (collect-append (#M(lambda (line)
                                          (collect ’list (#Mdecode-move
                                                           (#Mstring (scan ’string line)))))
                                        (choose moves)))))
      (declare (ignore blank-lines))
      (values (make-grid (length grid-lines) (length (first grid-lines)) :initial-contents grid-lines)
              move-list))))

(defun can-move-to? (grid coord delta)
  "True if location on grid at coord is empty, or item at location can move in direction."
  (and (on-grid? grid coord)
       (or (eql (grid-ref grid coord) ’\.)
           (can-move? grid coord delta))))

(defun can-move? (grid coord delta)
  "True if item on grid at coord can move in direction."
  (and (on-grid? grid coord)
       (ecase (grid-ref grid coord)
         (\. (error "No item at coord."))
         (\# nil)
         (@ (let ((target (2v+ coord delta)))
               (can-move-to? grid target delta)))
         (O (let ((target (2v+ coord delta)))
               (can-move-to? grid target delta)))
         (\[ (if (or (equal delta +north+)
                      (equal delta +south+))
                  (let ((target1 (2v+ coord delta))
                        (target2 (2v+ (2v+ coord delta) +east+)))
                    (and (can-move-to? grid target1 delta)
                         (can-move-to? grid target2 delta)))
                  (let ((target (2v+ coord delta)))
                    (can-move-to? grid target delta))))
         (\] (if (or (equal delta +north+)
                      (equal delta +south+))
                  (let ((target1 (2v+ coord delta))
                        (target2 (2v+ (2v+ coord delta) +west+)))
                    (and (can-move-to? grid target1 delta)
                         (can-move-to? grid target2 delta)))
                  (let ((target (2v+ coord delta)))
                    (can-move-to? grid target delta)))))))

(defun move! (grid coord delta)
  "Move item on grid at coord in direction delta."
  (if (can-move? grid coord delta)
      (ecase (grid-ref grid coord)
        (\. (error "Cannot move empty locations."))
        (\# (error "Cannot move walls."))
        (@ (let ((target (2v+ coord delta)))
               (unless (eql (grid-ref grid target) ’\.)
                 (move! grid target delta))
               (setf (grid-ref grid target) ’@
                     (grid-ref grid coord) ’\.)
               target))

        (O (let ((target (2v+ coord delta)))
               (unless (eql (grid-ref grid target) ’\.)
                 (move! grid target delta))
               (setf (grid-ref grid target) ’O
                     (grid-ref grid coord) ’\.)
               target))

        (\[ (let* ((targetl (2v+ coord delta))
                    (targetr (2v+ targetl +east+)))
               (unless (or (eql delta +east+)
                           (eql (grid-ref grid targetl) ’|.|))
                 (move! grid targetl delta))
               (unless (or (eql delta +west+)
                           (eql (grid-ref grid targetr) ’\.))
                 (move! grid targetr delta))
               (setf (grid-ref grid targetl) ’[
                     (grid-ref grid targetr) ’])
               (unless (eql delta +east+)
                 (setf (grid-ref grid (2v+ coord +east+)) ’\.))
               (unless (eql delta +west+)
                 (setf (grid-ref grid coord) ’\.))
               targetl))

        (\] (let* ((targetr (2v+ coord delta))
                    (targetl (2v+ targetr +west+)))
               (unless (or (eql delta +east+)
                           (eql (grid-ref grid targetl) ’\.))
                 (move! grid targetl delta))
               (unless (or (eql delta +west+)
                           (eql (grid-ref grid targetr) ’\.))
                 (move! grid targetr delta))
               (setf (grid-ref grid targetl) ’[
                     (grid-ref grid targetr) ’])
               (unless (eql delta +east+)
                 (setf (grid-ref grid coord) ’\.))
               (unless (eql delta +west+)
                 (setf (grid-ref grid (2v+ coord +west+)) ’\.))
           targetr))))
    coord))

(defun find-robot (grid)
  (collect-first
   (choose
    (mapping (((coord item) (scan-grid grid)))
      (when (eql item ’@)
        coord)))))

(defun score-map (grid)
  (collect-sum
   (mapping (((coord item) (scan-grid grid)))
     (if (or (eql item ’O)
             (eql item ’[))
         (+ (* (row coord) 100) (column coord))
         0))))

(defun show-grid (grid)
  (dotimes (row (grid-height grid))
    (dotimes (column (grid-width grid))
      (format t "~a" (grid-ref grid (coord column row))))
    (format t "~%")))

(defun puzzle (input-file wide?)
  (multiple-value-bind (grid moves) (read-input input-file wide?)
    (fold-left (lambda (robot move)
                 (move! grid robot move))
               (find-robot grid)
               moves)
    (score-map grid)))

(defun part-1 ()
  (puzzle (input-pathname) nil))

(defun part-2 ()
  (puzzle (input-pathname) t))

Joe Marshall: Advent of Code 2024: Day 14

via Planet Lisp by on Tue, 25 Feb 2025 08:00:00 GMT

For day 14, we are given the initial positions and velocities of a number of robots that walk a 101x103 grid. These are parsed with a regular expression:

(in-package "ADVENT2024/DAY14")

(defun read-input (input-file)
  (collect ’list
    (#M(lambda (line)
         (cl-ppcre:register-groups-bind ((#’parse-integer column) (#’parse-integer row)
                                         (#’parse-integer dx) (#’parse-integer dy))
             ("p=(\\d+),(\\d+)\\s+v=(-?\\d+),(-?\\d+)" line)
           (list (coord column row)
                 (coord dx dy))))
       (scan-file input-file #’read-line))))

The robots walk a grid linearly. They do not interact with each other, and they wrap when they cross the edge of the grid.

(defun step-n (width height coord velocity n)
  (2v-mod (2v+ coord (2v* n velocity)) (coord width height)))

For part 1, we are asked to multiply the number of robots in each quadrant after 100 steps in a 101 x 103 grid.

(defun quadrant (width height coord)
  (let ((half-width (floor width 2))
        (half-height (floor height 2)))
    (cond ((< (row coord) half-height)
           (cond ((< (column coord) half-width) 1)
                 ((> (column coord) half-width) 2)
                 (t nil)))
          ((> (row coord) half-height)
           (cond ((< (column coord) half-width) 3)
                 ((> (column coord) half-width) 4)
                 (t nil)))
          (t nil))))

(defparameter +grid-width+ 101)
(defparameter +grid-height+ 103)

(defun part-1 ()
  (let ((quadrants
          (#M(lambda (coord)
               (quadrant +grid-width+ +grid-height+ coord))
             (#M(lambda (robot)
                  (step-n +grid-width+ +grid-height+ (first robot) (second robot) 100))
                (scan 'list (read-input (input-pathname)))))))
    (* (collect-sum (#M(lambda (q) (if (eql q 1) 1 0)) quadrants))
       (collect-sum (#M(lambda (q) (if (eql q 2) 1 0)) quadrants))
       (collect-sum (#M(lambda (q) (if (eql q 3) 1 0)) quadrants))
       (collect-sum (#M(lambda (q) (if (eql q 4) 1 0)) quadrants)))))

We’re told that the robots form a picture of a Christmas tree after a certain number of steps. This was a bit tricky to figure out, but I figured that if the robots were clumped together in a picture, the number of empty rows and columns elsewhere would be maximized. Robots return to their starting point every 101 x 103 steps, so we only need to check the first 10403 steps.

(defun occupied-row? (locs row)
  (find row locs :test #’= :key #’row))

(defun occupied-column? (locs column)
  (find column locs :test #’= :key #’column))

(defun score (locs)
  (+ (collect-length
       (choose-if #’not
         (#Moccupied-row? (series locs) (scan-range :from 0 :below +grid-height+))))
     (collect-length
       (choose-if #’not
         (#Moccupied-column? (series locs) (scan-range :from 0 :below +grid-width+))))))

(defun part-2 ()
  (let ((robots (read-input (input-pathname))))
    (caar
     (sort
      (collect ’list
        (#M(lambda (n)
             (cons n (score (map ’list (lambda (robot)
                                         (step-n +grid-width+ +grid-height+ 
                                                 (first robot) (second robot) n))
                                 robots))))
           (scan-range :from 0 :below (* +grid-width+ +grid-height+))))
      #’> :key #’cdr))))